１．ANOVA1,2の位置付け
　ANOVA1,2は一つ又は二つの母平均の検定と推定、及び直交配列表実験の中間的な位置付けになる。ANOVA1,2の検定と推定の考え方は一つ又は二つの母平均の考え方を拡張したものであり、直交配列表実験における分散分析（ばらつきの分解）の考え方は、ANOVA1,2のばらつきの分解方法の考え方が基本になっている。正直エンジニアが目指す最終目標は直交配列表実験（若しくはそれ以上）なのでANOVA1,2はパスしても構わないのであるが、ばらつきの分解の考え方はシンプルな分わかり易く基本的な考え方はここで抑えておきたいところである。

２．一元配置法（ANOVA1）
2.1データの構造
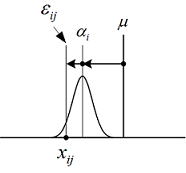
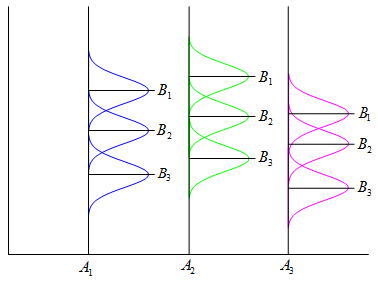
　特性値に影響を与える複数の要因からある因子Aについて三つの条件（3水準：A₁, A₂, A₃）を設定し、各条件でr 回の実験をランダマイズに実施したものとする。この場合は三つの母集団を想定したことになり、r 回の実験とはそれらの母集団からr 個抜き取ったサンプルと見なせる。A_i水準の母平均をμ_iとし更にμiを全体の平均（一般平均と呼ぶ）μと因子A_iの効果をa_iで表すと、一元配置のデータ構造式（A_i水準の任意データx_ij）は以下のように表せる。因子Aの効果は一般平均から各水準間までのずれ量となるが、そのΣを取ると相殺されてゼロとなる。
　
　
　　
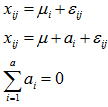
　実験計画法では何れの手法も仮説をたてることはしないが、分散分析では結果としてF検定を実施していることになり仮に仮説をたてるとするなら、母平均に差がある（つまり因子Aの効果はある）ことを立証したいことから、仮説の設定は棄却側にそれを謳う内容になる。
　帰無仮説 Ｈ₀：因子Aの効果はない（a₁=a₂=a₃=0）
　対立仮説 Ｈ₁：因子Aの効果はある（少なくとも一つはa_i≠0）
2.2ばらつき（平方和）の分解
　一元配置におけるデータのばらつきがどのように生じているかを考えると、下図に示すように因子Aの効果（水準の違い）と偶然的に発生する誤差（ε_ij）により生じることが分かる。データの構造式からA_i水準の任意のデータx_ijは以下のように表せる。

　
　
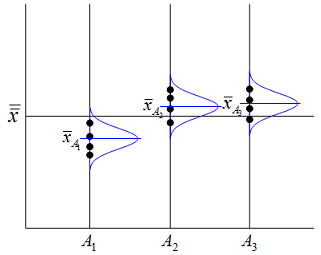
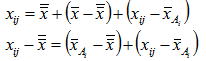
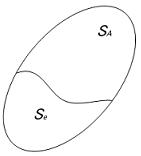
　左辺は個々のデータと一般平均の偏差であり、右辺の第一項は因子Aの効果によるばらつき第二項は実験誤差そのものであり、個々のばらつきはこれらのばらつきに分解できることを表している。上の式は1個のデータを表したものであるが、各辺を2乗して全てのi，j について加えると以下のように平方和の形で表現できる。ここに左辺は総平方和であり右辺は水準間平方和（S_A：因子Aの水準効果でありのばらつき具合を表す）と誤差平方和（S_e：同一水準内における実験誤差によるばらつき）になる。つまり下図のように総平方和は水準間平方和（S_A）と、誤差平方和（S_e）に分解できることになる。
　
　
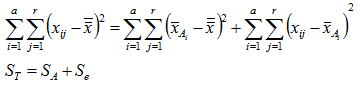
2.3分散分析表
　総平方和を水準間平方和と誤差平方和に分解し以下の仮説を検定する行為を分散分析という。検定を行う際は二つの平方和（S_A,S_e）をそれぞれの自由度で割った分散比（F₀値）の大きさで比較する。この考え方は二つの母集団（水準の違いによるばらつきと誤差によるばらつき）における分散比のF検定と同様である。ここでのポイントは、2.1項に述べてあるように知りたい情報は母平均に差があるかであるが、実際の検定行為はF検定となっている点であり以下にこの点について説明する。
　H₀：因子Aの効果はない（a₁=a₂=a₃=0）
　H₁：因子Aの効果はある（少なくとも一つはa_i≠0）
　当初の仮説は母平均に差があるや否やを観点としたものであるが、これを母平均のばらつき具合として捉えれば上の仮説は以下のように置き換えることができる。
　H₀：母平均のばらつきは小さい（σ_A²=0　⇔　E（V_A）=E（Ve））
　H₁：母平均のばらつきは大きい（σ_A²＞0　⇔　E（V_A）＞E（Ve））
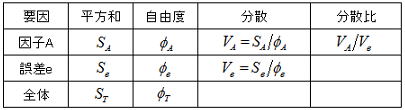
　更に分散を比率の大きさで捉えるとするならH₀はF₀=V_A/V_e=1、H₁はF₀=V_A/V_e＞1と表せ、最終的に母平均に差があるや否やは分散比の大きさで評価できることになり、これらの情報を纏めた一覧表が分散分析表と呼ばれるものである。平方和の求め方は2.2項に説明した通りであるが、分散分析表における一番のポイントは自由度の考え方であろう。自由度の考え方は別項を参照頂くとして、得られたn個のサンプルデータから基本統計量（平均、変動、分散、標準偏差、範囲）を求める際に、平均の自由度がn個であるのに対して分散の自由度は（n-1）個であることに注目すれば、分散分析表における自由度も同様に考えることができる。すなわち因子Aのデータ個数は因子Aの水準数（a）であり全体のデータ個数は総データ数（a×r =N）であることから、φ_Aとφ_Tはそれぞれのデータ個数から1を引くことで求められ、これにより誤差の自由度も以下のように決定する。
　
　　
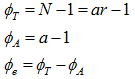
2.4分散分析後の検討評価
1)検定結果の意味
　求められた分散比（F₀）を以下に示す検定値により検定することになる。
　　：H₀を採択
　　：H₀を棄却
　検定結果を図で表すと以下のようになる。帰無仮説が採択されるとは左図の状況を表しており因子Aの条件を変化させても特性値に変化がないということである。一方帰無仮説が棄却されるとは右図の状況を表しており、因子Aの条件により特性値は影響を受ける（効果がある）との判断になる。この状況を具体的な数値として知るためには、各水準の母平均及び任意の2水準間の差の推定を行う必要がある。
　
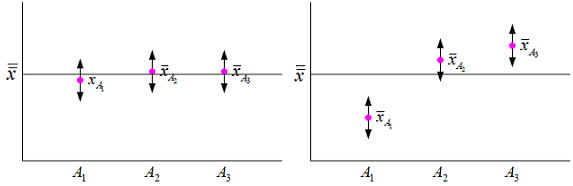
2)母平均の推定と母平均の差の推定
　因子Aの各水準の母平均及び任意の2水準間の差と、それぞれの（1-α）信頼区間は以下のように求められる。任意の2水準間に差があるかを検定（母分散が未知で等分散と考えられる場合）するには、水準間の差の大きさと最小有意差（lsd.：least significant difference）を比較することで棄却判断が得られる。
　
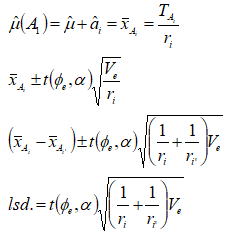
3)誤差の大きさの検討
　先ず誤差分散の期待値を検討してみよう。誤差の平方和からの展開式によりS_eとV_eの期待値は以下のように求められる。これらの理論証明は少し複雑ではあるが、我々は最後の式の結果さえ知っていればそれで十分である。この式（誤差分散の期待値の結果）は、誤差分散が母標準偏差の推定量を導く値であることを示しており、この値により特性（Y）のばらつきの妥当性が検証できることを意味している。分散分析は母平均の情報しか得られないと思われがちだが、ばらつきの情報も得られることを認識しておく必要がある。この値が予測された範囲に収まっている（設計の本質に依存している）かの判断は、実験担当者が技術的見地から判断する以外にないが、V_eが妥当な値で且つ有意な因子は量産規模でも十分効果があると判断できる。
　　

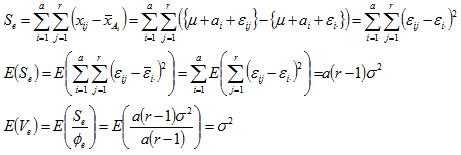
３．二元配置法（ANOVA2）
3.1データの構造
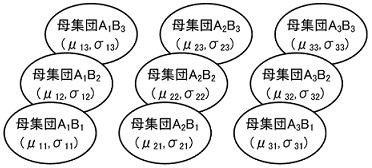
　実験で取り上げる因子が単独な場合が一元配置法であるが、二元配置法では取り上げる因子数は2因子となる。二元配置法では繰り返しがある場合と繰り返しがない場合があるが、ここでは適用頻度が高い繰り返しがある場合を取り上げる。特性値に影響を与える複数の要因から二つの因子A,Bを取り上げ、各三つの条件を設定しr回の実験をランダマイズに実施したものとする。この場合は9個の母集団が想定され、データはそれらの母集団からr個抜き取ったサンプルと見なせる。A_iB_i水準の任意データx_ijkはその母平均をμ_ijとすると以下のように表される。更にμ_ijを全体の平均（一般平均と呼ぶ）μと因子Aの効果をa_i、因子Bの効果をb_j、更に交互作用（A×B）の効果を(ab)_ijとすると、二元配置のデータ構造式は以下のように表せる。 因子A,B,(A×B)の効果は一般平均から各水準間までのずれのΣを取ると、一元配置同様に相殺されてゼロとなる。

　
　
　
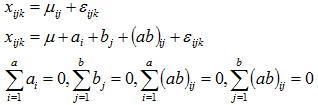
3.2ばらつき（平方和）の分解
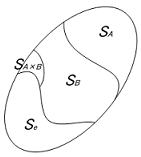
　データの構造式において一般平均を左辺に移し、交互作用以外の項を一般平均を用いて表すと以下のように表せる。交互作用は以下のように定義されるのでこれを代入し、各辺を2乗して全てのi，j，k について加えると、一元配置同様に平方和の形で表現できる。左辺は個々のデータの全変動（総平方和）、右辺の第一項は因子Aの効果によるばらつき、第二項は因子Bの効果によるばらつき、第三項は交互作用の効果によるばらつき、第四項は実験誤差であることから一元配置同様に全変動はこれらのばらつきに分解できる。
　
　
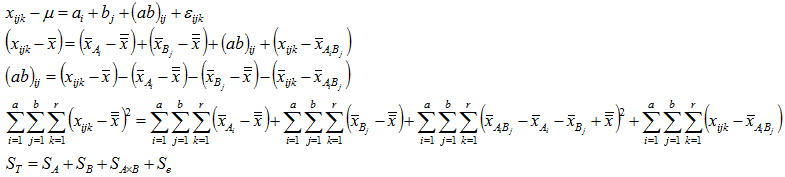
3.3分散分析表
　一元配置同様に6.1項の各母平均に差があるかについて仮説を設定してみよう。
　　H₀：因子Aの効果はない（a₁=a₂=a₃=0）
　　H₀：因子Bの効果はない（b₁=b₂=b₃=0）
　　H₀：交互作用（A×B）はない（ab₁₁=ab₁₂=・・・=ab₃₃=0）
　　H₁：因子*の効果はある（少なくとも一つは*_i≠0）
　　H₁：交互作用（A×B）はある（少なくとも一つはab_ij≠0）
　一元配置と同様に母平均に差があるや否やを母平均のばらつき具合として捉え、上の仮説を以下のように置き換え各要因の分散と誤差分散の比（F₀=V_*/V_e）を用いてF検定を実施する。
　　H₀：母平均のばらつきは小さい（σ_A²=0　⇔　E（V_A）=E（V_e））
　　H₀：母平均のばらつきは小さい（σ_B²=0　⇔　E（V_B）=E（V_e））
　　H₀：母平均のばらつきは小さい（σ_A×B²=0　⇔　E（V_A×B）=E（V_e））
　自由度の考え方も一元配置と同様であるが、要因として交互作用があるため以下のようになる。
　　
　
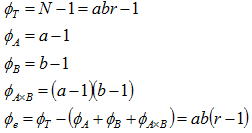
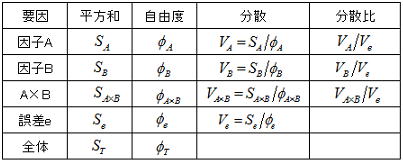
3.4分散分析後の検討評価
1)検定結果の意味
　求められた分散比（F₀）を以下に示す検定値により検定することになる。
　　：H₀を採択
　　：H₀を棄却
　　：H₀を採択
　　：H₀を棄却
　　：H₀を採択
　　：H₀を棄却
　交互作用が有意でない（一般的にはF₀≦1.0～2.0が目安）場合は、以下の式により交互作用の平方和を誤差に繰り入れるプーリングという操作を行い再度分散分析を行う。プーリングにより誤差分散と自由度を大きくしても有意な要因はその効果の確実性が高いということになり、つまり高い検出力で検定結果が得られることになる。
　
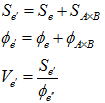
2)母平均の推定と母平均の差の推定
　分散分析後の母平均の推定やその区間推定では交互作用をプーリングしたかどうか（つまり交互作用が有意であるや否や）で異なるため、これらは分けて考える必要がある。
●交互作用がない場合
　交互作用がない場合の母平均の推定は、各因子の単独水準と組み合わせ条件の両方で推定することになり、それぞれの（1-α）の信頼区間は下記式で求められる。なおn_eは有効反復数といい以下の式は「伊奈の公式」と呼ばれている。
　
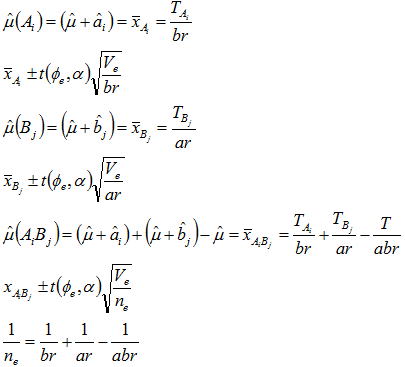
●交互作用がある場合
　交互作用がある場合は各因子の単独水準の母平均を推定しても意味がなく、各因子の組み合わせ水準で母平均を推定することになりその（1-α）の信頼区間は下記式となる。
　
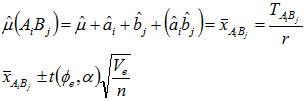
3)誤差の大きさの検討
　一元配置の誤差分散の期待値の式にあるように、誤差分散は母標準偏差の推定量を導く値であることは変わらず、この値が予測された範囲に収まっている（設計の本質に依存している）かの検討は重要である。